 |
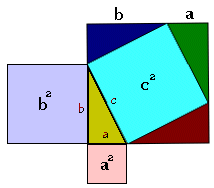
มี รูป รูป ดัง a2 + 2ab + b2 = c2 + 2ab นั่น |
ที่มา : รศ. ยืน ภู่วรวรรณ, สำนักบริการคอมพิวเตอร์ มหาวิทยาลัยเกษตรศาสตร์

มี
รูป
รูป
ดัง
a2 + 2ab + b2
= c2 + 2ab
นั่น
ที่มา : รศ. ยืน ภู่วรวรรณ, สำนักบริการคอมพิวเตอร์ มหาวิทยาลัยเกษตรศาสตร์