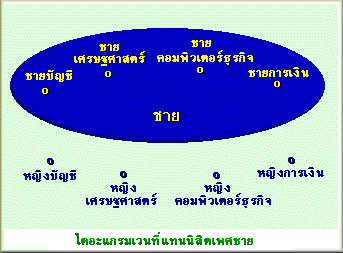
 |
บัญชี | เศรษฐศาสตร์ | การ | คอมพิวเตอร์ |
| ชาย | 330 | 360 | 90 | 120 |
| หญิง | 120 | 390 | 60 | 30 |
| 1. ความ |
| 2. ความ |
| 3. ความ |
 |
บัญชี | เศรษฐศาสตร์ | การ | คอมพิวเตอร์ |
| ชาย | 0.22 | 0.24 | 0.06 | 0.08 |
| หญิง | 0.08 | 0.26 | 0.04 | 0.02 |
| P(เศรษฐศาสตร์) | = P(นิสิต = 0.24 + 0.26 = 0.5 |
| P(ชาย) | = 0.22 + 0.24 + 0.06 + 0.08 = 0.6 |
| P(นิสิต | = 0.26 + 0.04 = 0.3 |
| ผู้ | ร้อย |
| ผู้ | ร้อย |
| ผู้ | ร้อย |
| ผู้ | ร้อย |
| ผู้ | ร้อย |
| ปรากฏว่า | 6 คะแนน |

| สมมุติ | x คน |
| ผู้ | y คน |
| จำนวน | 100 คน |
ดัง | |
| x + y + 20 + 13 + 12 + 15 + 9 | = 100 คน |
| x + y | = 31 คน |
| ผู้ | 6 คน |
| (x + 20 + 13 + 12) - (y + 20 + 13 + 15) | = 6 คน |
| x - y | = 9 คน |
| (1) + (2) ---> 2x | = 40 คน |
| x | = 20 คน |
| y | = 11 คน |
ดัง | |
| คน | = 65 คน |
| คน | = 59 คน |
| คน | = 49 คน |
ที่มา : รศ. ยืน ภู่วรวรรณ, สำนักบริการคอมพิวเตอร์ มหาวิทยาลัยเกษตรศาสตร์