|
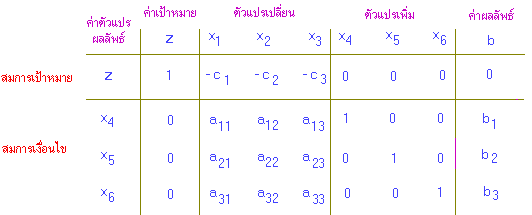
| Z -- c1x1 -- c2x2 -- c3x3
|
|
|
| = |
| a11x1 + a12x2 + a13x3
| + x4
|
|
| = |
| a21x1 + a22x2 + a23x3
|
| + x5
|
| = |
| a31x1 + a32x2 + a33x3
|
|
| + x6
| = | | |||||||||||
|
|
|
| Max Z = c1x1 + c2x2 + c3x3
|
| a11x1 + a12x2 + a13x3
| <
| b1
|
| a21x1 + a22x2 + a23x3
| <
| b2
|
| a31x1 + a32x2 + a33x3
| <
| b3
| | |||||
|
| Z -- c1x1 -- c2x2 -- c3x3
|
|
|
| = |
| a11x1 + a12x2 + a13x3
| + x4
|
|
| = |
| a21x1 + a22x2 + a23x3
|
| + x5
|
| = |
| a31x1 + a32x2 + a33x3
|
|
| + x6
| = | | |||||||||||
|
|
 z - c1x1 - c2x2 - c3x3 = 0
z - c1x1 - c2x2 - c3x3 = 0
 จะ จะ
|
|
 x4 = b1 x5 = b2 x6 = b3 x4 = b1 x5 = b2 x6 = b3
b1/a12

|